Tsz On Mario Chan

Cousin-quasi-tori are non-compact analogue of compact complex tori which have no non-constant holomorphic functions on them and are weakly pseudoconvex. Without harmonic theory at the disposal, I will show how a vanishing theorem for the cohomology of holomorphic line bundles on Cousin-quasi-tori is proved by solving 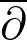-equations using the classical 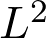method and a Runge-type approximation. The result generalises Mumford's Index Theorem on compact complex tori and gives a finer vanishing result than that given by the theorem of Andreotti and Grauert.