A vanishing theorem for Cousin-quasi-tori
Lundi, 2 Mai, 2016 - 10:30
Résumé :
Cousin-quasi-tori are non-compact analogue of compact complex tori which have no non-constant holomorphic functions on them and are weakly pseudoconvex. Without harmonic theory at the disposal, I will show how a vanishing theorem for the cohomology of holomorphic line bundles on Cousin-quasi-tori is proved by solving 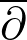 -equations using the classical
-equations using the classical 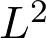 method and a Runge-type approximation. The result generalises Mumford's Index Theorem on compact complex tori and gives a finer vanishing result than that given by the theorem of Andreotti and Grauert.
method and a Runge-type approximation. The result generalises Mumford's Index Theorem on compact complex tori and gives a finer vanishing result than that given by the theorem of Andreotti and Grauert.
Institution de l'orateur :
NCTS Taïwan
Thème de recherche :
Algèbre et géométries
Salle :
4

